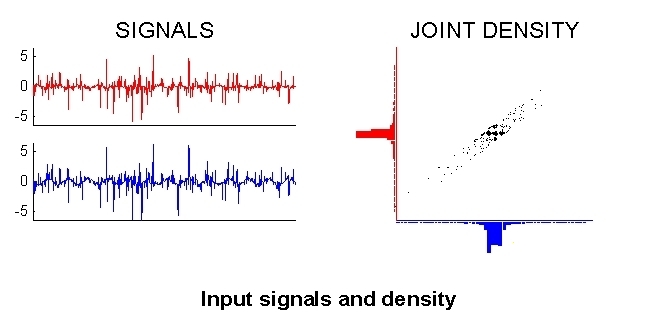
A first step in many ICA algorithms is to whiten (sphere) the data. This means that we remove any correlations in the data, i.e. the signals are forced to be uncorrelated. Again putting the words in mathematical terms, we seek a linear transformation V such that when y = Vx we now have E{yy'} = I. This is easily accomplished by setting V = C-1/2, where C = E{xx'} is the correlation matrix of the data, since then we have E{yy'} = E{Vxx'V'} = C-1/2CC-1/2 = I.
The figure below shows the signals y and the joint density p(y) after such an operation.
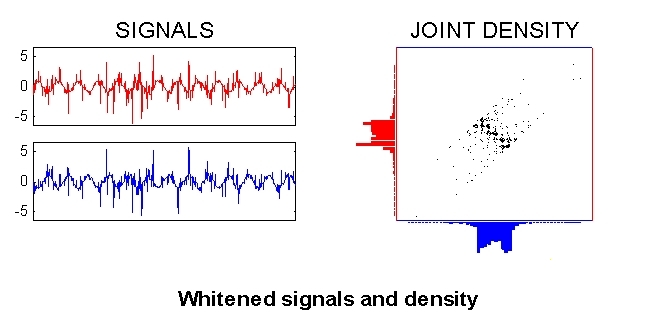
After sphering, the separated signals can be found by an orthogonal transformation of the whitened signals y (this is simply a rotation of the joint density). The appropriate rotation is sought by maximizing the non-normality of the marginal densities (shown on the edges of the density plot). This is because of the fact that a linear mixture of independent random variables is necessarily more Gaussian than the original variables. (This is the same phenomenon as is stated by the central limit theorem.) This implies that in ICA we must restrict ourselves to at most one Gaussian source signal.
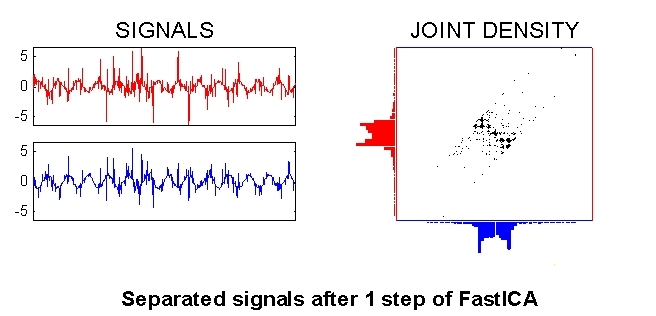
There are many algorithms for performing ICA, but the most efficient to date is the FastICA. (fixed-point) algorithm which was developed by us. The plot below shows the result after one step of the FastICA algorithm.
The rotation continues...
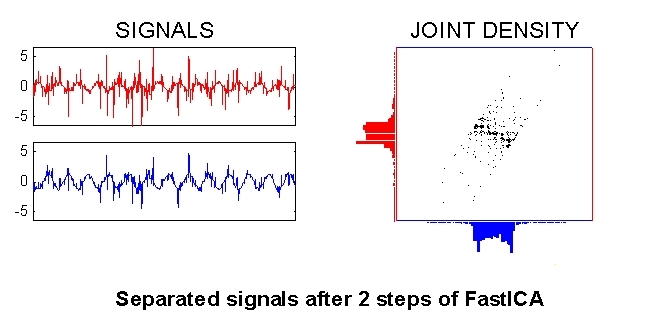
...and continues...
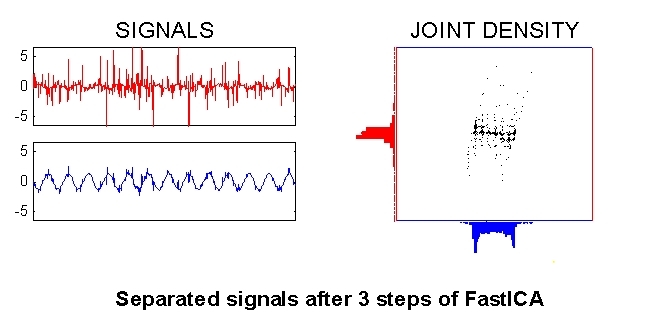
...until it starts to converge...
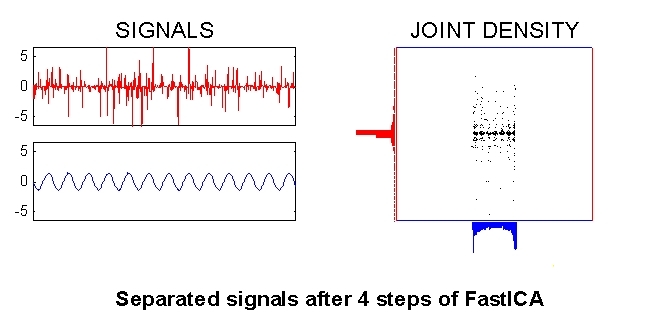
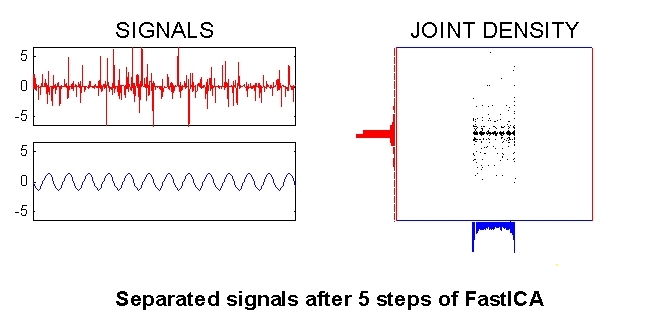
Convergence! The source signals (components of s) in this example were a sinusoid and impulsive noise, as can be seen in the left part of the plot below. The right plot shows the joint density which can be seen to be the product of the marginal densities, i.e. p(s)=p(s1)p(s2). This is of course the definition of independence.